Математична складність завдання полягала у тому, що необхідно було…
Лотерея – це спосіб випробувати свою вдачу і отримати виграш, але чи може математика допомогти вам зрозуміти ймовірність успіху у цій грі? Як пише видання Iflscience, дослідники з Університету Манчестера розробили інноваційний підхід, щоб визначити, яка мінімальна кількість лотерейних квитків потрібна для гарантованого виграшу. Однак, навіть з такою науково обґрунтованою стратегією, лотерея залишається ігрою випадку, де успіх не гарантований.
Гра «Лото» Національної лотереї Великобританії вже давно цікавить людей, але дослідники докладно проаналізували її правила. Головна мета гравця – вгадати шість чисел від 1 до 59, які розігрує компанія. Зараз джекпот становить приголомшливі $9,9 млн.
Математики Девід Стюарт і Девід Кушинг знайшли найефективніший спосіб гарантувати виграш у цій грі. Вони використали площини Фано – геометричні фігури, які вони використали для опису можливих комбінацій чисел. Це дає можливість визначити мінімальну кількість квитків для гарантованого виграшу. Вони довели, що лише 27 квитків дозволять вам гарантовано отримати принаймні два числа зі всіх 45 057 474 можливих комбінацій.
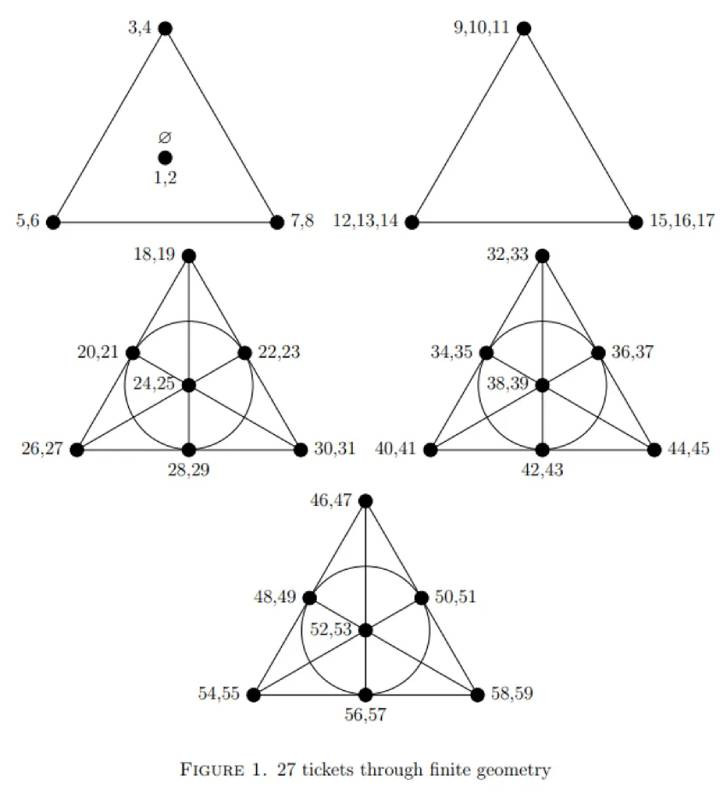
Фото: Манчестерський університет
Математична складність завдання полягала у тому, що необхідно було враховувати те, що деякі числа не можуть з'являтися разом на одному квитку. Це призвело до створення теорії графів, де вони довели існування незалежного набору розміром шість. Таким чином, їхній підхід дозволяє гарантувати виграш у лотереї.
Не зважаючи на це відкриття, варто пам'ятати, що лотерея залишається грою випадку. Навіть з математичним підходом до вибору квитків, шанси на виграш залишаються невеликими. Математик Пітер Роулетт наголошує, що у 99% випадків інвестиції в лотерею не призводять до прибутку.
І все ж, дослідники вирішили перевірити свою теорію на практиці. Вони придбали 27 лотерейних квитків перед одним із розіграшів. Ця спроба не призвела до успіху – жлден з їхніх квитків не став виграшним. Це підкреслює, що навіть з математичним розрахунком, лотерея залишається ігрою випадку.
Таким чином, математичний аналіз може надати цікаві підходи для розуміння ймовірності виграшу в лотереї, але не забувайте, що успіх тут все ще залежить від удачі. Лотерея може бути захопливою розвагою, але не гарантує фінансового виграшу.
Читайте також:

